go 实现十大经典排序算法
·
giftia
1.冒泡排序 (Bubble Sort)

package main
import "fmt"
func main() {
in := []int{3, 8, 4, 4, 9, 2}
BubbleSort(in)
fmt.Println(in) // [2 3 4 4 8 9]
}
func BubbleSort(a []int) {
for i := 0; i < len(a); i++ {
for j := 0; j < len(a)-i-1; j++ {
if a[j] > a[j+1] {
a[j], a[j+1] = a[j+1], a[j]
}
}
}
}
- 最坏情况:O(n²),当列表是逆序时。
- 最好情况:O(n),当列表已经有序时。
- 平均情况:O(n²)。
2.选择排序 (Selection Sort)

package main
import "fmt"
func main() {
in := []int{3, 8, 4, 4, 9, 2}
SelectionSort(in)
fmt.Println(in) // [2 3 4 4 8 9]
}
func SelectionSort(a []int) {
for i := 0; i < len(a)-1; i++ {
minIndex := i
for j := i + 1; j < len(a); j++ {
if a[j] < a[minIndex] {
minIndex = j
}
}
if minIndex != i { // 避免不必要的交换
a[i], a[minIndex] = a[minIndex], a[i]
}
}
}
- 最坏情况:O(n²),无论输入数据是否有序,都需要进行 n(n-1)/2 次比较。
- 最好情况:O(n²),即使列表已经有序,仍需进行相同数量的比较。
- 平均情况:O(n²)。
3.插入排序 (Insertion Sort)

package main
import "fmt"
func main() {
in := []int{3, 8, 4, 4, 9, 2}
InsertionSort(in)
fmt.Println(in) // [2 3 4 4 8 9]
}
func InsertionSort(a []int) {
for i := 1; i < len(a); i++ {
current := a[i]
j := i - 1
for j >= 0 && current < a[j] { // 比现在大的元素依次后移
a[j+1] = a[j]
j--
}
a[j+1] = current
}
}
- 最坏情况:O(n²),当列表是逆序时,每次插入都需要移动所有已排序元素。
- 最好情况:O(n),当列表已经有序时,只需遍历一次列表。
- 平均情况:O(n²)。
4.希尔排序 (Shell Sort)

- 选择增量序列:选择一个增量序列(gap sequence),用于将列表分成若干子列表。常见的增量序列有希尔增量(n/2, n/4, …, 1)等。
- 分组插入排序:按照增量序列将列表分成若干子列表,对每个子列表进行插入排序。
- 缩小增量:逐步缩小增量,重复上述分组和排序过程,直到增量为 1。
- 最终排序:当增量为 1 时,对整个列表进行一次插入排序,完成排序。
package main
import "fmt"
func main() {
in := []int{3, 8, 4, 4, 9, 2}
ShellSort(in)
fmt.Println(in) // [2 3 4 4 8 9]
}
func ShellSort(a []int) {
n := len(a)
// 使用Knuth增量序列 h = 3*h + 1
h := 1
for h < n/3 {
h = 3*h + 1 // 1, 4, 13, 40, 121, ...
}
for h >= 1 {
// 以间隔 h 对数组进行排序
for i := h; i < n; i++ {
// 对每个间隔h的子序列进行插入排序
for j := i; j >= h && a[j] < a[j-h]; j -= h {
a[j], a[j-h] = a[j-h], a[j]
}
}
h /= 3 // 减小间隔
}
}
- 最坏情况:O(n²),当增量序列选择不当时。
- 最好情况:O(n log n),当增量序列选择合适时。
- 平均情况:O(n log n) 到 O(n²) 之间。
5.归并排序 (Merge Sort)

- 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置;
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
- 重复步骤 3 直到某一指针达到序列尾;
- 将另一序列剩下的所有元素直接复制到合并序列尾。
package main
import "fmt"
func main() {
in := []int{3, 8, 4, 4, 9, 2}
result := MergeSort(in)
fmt.Println(result) // [2 3 4 4 8 9]
}
// MergeSort 归并排序主函数,返回新的有序数组
func MergeSort(arr []int) []int {
if len(arr) <= 1 {
return arr // 基本情况:数组长度为0或1时直接返回
}
// 分割数组
mid := len(arr) / 2
left := MergeSort(arr[:mid]) // 递归排序左半部分
right := MergeSort(arr[mid:]) // 递归排序右半部分
// 合并已排序的两部分
return merge(left, right)
}
// merge 合并两个有序数组
func merge(left, right []int) []int {
merged := make([]int, 0, len(left)+len(right))
i, j := 0, 0
// 比较两个数组元素,按顺序添加到merged
for i < len(left) && j < len(right) {
if left[i] <= right[j] {
merged = append(merged, left[i])
i++
} else {
merged = append(merged, right[j])
j++
}
}
// 添加剩余元素
merged = append(merged, left[i:]...)
merged = append(merged, right[j:]...)
return merged
}
- 分解:每次将列表分成两半,需要 O(log n) 层递归。
- 合并:每层递归需要 O(n) 的时间来合并子列表。
- 总时间复杂度:O(n log n)。
6.快速排序 (Quick Sort)

- 选择基准元素:从列表中选择一个元素作为基准(pivot)。选择方式可以是第一个元素、最后一个元素、中间元素或随机元素。
- 分区:将列表重新排列,使得所有小于基准元素的元素都在基准的左侧,所有大于基准元素的元素都在基准的右侧。基准元素的位置在分区完成后确定。
- 递归排序:对基准元素左侧和右侧的子列表分别递归地进行快速排序。
- 合并:由于分区操作是原地进行的,递归结束后整个列表已经有序。
package main
import (
"fmt"
"math/rand"
"time"
)
func main() {
in := []int{3, 8, 4, 4, 9, 2}
QuickSort(in, 0, len(in)-1)
fmt.Println(in) // 输出: [2 3 4 4 8 9]
in = []int{3, 8, 4, 4, 9, 2}
QuickSortPlus(in, 0, len(in)-1)
fmt.Println(in) // 输出: [2 3 4 4 8 9]
}
// 快排
func QuickSort(arr []int, left, right int) {
if left >= right {
return
}
// 随机选择基准点
rand.Seed(time.Now().UnixNano())
index := rand.Intn(right-left+1) + left
pivot := arr[index]
// 将基准点交换到最右侧,简化分区逻辑
arr[index], arr[right] = arr[right], arr[index]
temp := left // 边界,一开始在左边
for i := left; i < right; i++ { // 现在right位置是基准点,不需要处理
if arr[i] < pivot {
arr[temp], arr[i] = arr[i], arr[temp]
temp++
}
}
// 将基准点放到正确位置
arr[temp], arr[right] = arr[right], arr[temp]
QuickSort(arr, left, temp-1)
QuickSort(arr, temp+1, right)
}
// 三路快排
func QuickSortPlus(arr []int, left, right int) {
if left >= right {
return
}
// 随机选择基准点
rand.Seed(time.Now().UnixNano())
index := rand.Intn(right-left+1) + left
pivot := arr[index]
temp1, temp2 := left, right // 两个边界
i := left
for i <= temp2 {
if arr[i] == pivot {
i++
} else if arr[i] < pivot {
arr[temp1], arr[i] = arr[i], arr[temp1]
i++
temp1++
} else {
arr[temp2], arr[i] = arr[i], arr[temp2]
temp2--
}
}
QuickSortPlus(arr, left, temp1-1)
QuickSortPlus(arr, temp2+1, right)
}
- 分解:每次将列表分成两半,需要 O(log n) 层递归。
- 合并:每层递归需要 O(n) 的时间来合并子列表。
- 总时间复杂度:O(n log n)。
7.堆排序 (Heap Sort)

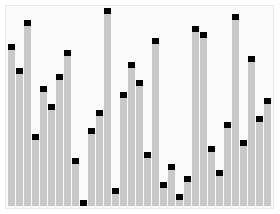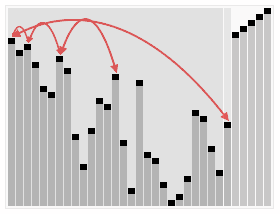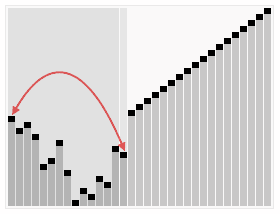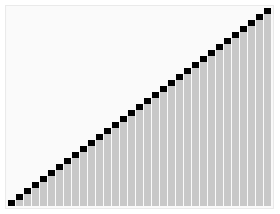
- 创建一个堆 H[0……n-1];
- 把堆首(最大值)和堆尾互换;
- 把堆的尺寸缩小 1,并调用 shift_down(0),目的是把新的数组顶端数据调整到相应位置;
- 重复步骤 2,直到堆的尺寸为 1。
package main
import "fmt"
func main() {
in := []int{3, 8, 4, 4, 9, 2}
HeapSort(in)
fmt.Println(in) // 输出: [2 3 4 4 8 9]
}
// HeapSort 堆排序主函数
func HeapSort(arr []int) {
n := len(arr)
if n <= 1 {
return
}
// 构建最大堆
for i := n/2 - 1; i >= 0; i-- {
heapify(arr, n, i)
}
// 一个个交换元素
for i := n - 1; i > 0; i-- {
arr[0], arr[i] = arr[i], arr[0] // 将堆顶元素(最大值)与当前未排序部分的最后一个元素交换
heapify(arr, i, 0) // 重新调整堆,排除已排序的元素
}
}
// heapify 将以i为根的子树调整为最大堆
func heapify(arr []int, n, i int) {
largest := i // 初始化根节点为最大值
left := 2*i + 1 // 左子节点
right := 2*i + 2 // 右子节点
// 如果左子节点大于根节点
if left < n && arr[left] > arr[largest] {
largest = left
}
// 如果右子节点大于当前最大值
if right < n && arr[right] > arr[largest] {
largest = right
}
// 如果最大值不是根节点,则交换并继续调整子树
if largest != i {
arr[i], arr[largest] = arr[largest], arr[i]
heapify(arr, n, largest) // 递归调整受影响的子树
}
}
- 构建最大堆:O(n)。
- 每次调整堆:O(log n),总共需要调整 n-1 次。
- 总时间复杂度:O(n log n)。****
8.计数排序 (Counting Sort)

- 统计频率:遍历待排序的列表,统计每个元素出现的次数,存储在一个计数数组中。
- 累加频率:将计数数组中的值累加,得到每个元素在排序后列表中的最后一个位置。
- 构建有序列表:遍历待排序的列表,根据计数数组中的位置信息,将元素放到正确的位置。
- 输出结果:将排序后的列表输出。
package main
import "fmt"
func main() {
in := []int{3, 8, 4, 4, 9, 2}
CountingSort(in)
fmt.Println(in) // 输出: [2 3 4 4 8 9]
}
// CountingSort 计数排序主函数
func CountingSort(arr []int) {
if len(arr) <= 1 {
return
}
// 找出最大值和最小值
min, max := arr[0], arr[0]
for _, num := range arr {
if num < min {
min = num
}
if num > max {
max = num
}
}
// 计算计数数组的长度
countLen := max - min + 1
count := make([]int, countLen)
// 统计每个元素出现的次数
for _, num := range arr {
count[num-min]++
}
// 将统计结果放回原数组
index := 0
for i := 0; i < countLen; i++ {
for count[i] > 0 {
arr[index] = i + min
index++
count[i]--
}
}
}
- 统计频率:O(n),遍历列表一次。
- 累加频率:O(k),遍历计数数组一次。
- 放置元素:O(n),遍历列表一次。
- 总时间复杂度:O(n + k),其中 n 是列表长度,k 是数据的范围大小。
9.桶排序 (Bucket Sort)
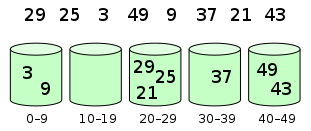

- 初始化桶:根据数据的范围和分布,创建若干个桶。
- 分配元素:遍历待排序的列表,将每个元素分配到对应的桶中。
- 排序每个桶:对每个桶中的元素进行排序(可以使用插入排序、快速排序等)。
- 合并桶:将所有桶中的元素按顺序合并,得到最终排序结果。
package main
import (
"fmt"
"sort"
)
func main() {
in := []float64{0.42, 0.32, 0.33, 0.52, 0.37, 0.47, 0.51}
BucketSort(in)
fmt.Println(in) // 输出: [0.32 0.33 0.37 0.42 0.47 0.51 0.52]
}
// BucketSort 桶排序主函数(处理0.0~1.0之间的浮点数)
func BucketSort(arr []float64) {
if len(arr) <= 1 {
return
}
// 创建桶
n := len(arr)
buckets := make([][]float64, n)
// 将元素分配到桶中
for _, num := range arr {
index := int(num * float64(n)) // 确定元素所在的桶
buckets[index] = append(buckets[index], num)
}
// 对每个桶内的元素进行排序
for _, bucket := range buckets {
sort.Float64s(bucket) // 使用标准库排序
}
// 合并所有桶的结果
index := 0
for _, bucket := range buckets {
for _, num := range bucket {
arr[index] = num
index++
}
}
}
- 分配元素:O(n),遍历列表一次。
- 排序每个桶:假设每个桶中的元素数量为 m,则排序一个桶的时间复杂度为 O(m log m)。如果桶的数量为 k,则总时间复杂度为 O(k * m log m)。
- 合并桶:O(n),遍历所有桶一次。
- 总时间复杂度:O(n + k * m log m),其中 n 是列表长度,k 是桶的数量,m 是每个桶的平均元素数量。
10.基数排序 (Radix Sort)

- 确定最大位数:找到列表中最大数字的位数,确定需要排序的轮数。
- 按位排序:从最低位开始,依次对每一位进行排序(通常使用计数排序或桶排序作为子排序算法)。
- 合并结果:每一轮排序后,更新列表的顺序,直到所有位数排序完成。
package main
import "fmt"
func main() {
in := []int{3, 8, 4, 4, 9, 2}
RadixSort(in)
fmt.Println(in) // 输出: [2 3 4 4 8 9]
}
// RadixSort 基数排序主函数
func RadixSort(arr []int) {
if len(arr) <= 1 {
return
}
// 找出最大值以确定位数
max := arr[0]
for _, num := range arr {
if num > max {
max = num
}
}
// 从最低位(个位)到最高位进行排序
for exp := 1; max/exp > 0; exp *= 10 {
countingSortByDigit(arr, exp)
}
}
// countingSortByDigit 根据指定位上的数字进行计数排序
func countingSortByDigit(arr []int, exp int) {
n := len(arr)
output := make([]int, n)
count := make([]int, 10) // 0-9 共10个数字
// 统计每个位上的数字出现的次数
for i := 0; i < n; i++ {
digit := (arr[i] / exp) % 10
count[digit]++
}
// 计算累积次数
for i := 1; i < 10; i++ {
count[i] += count[i-1]
}
// 构建有序输出数组(从后向前遍历以保持稳定性)
for i := n - 1; i >= 0; i-- {
digit := (arr[i] / exp) % 10
output[count[digit]-1] = arr[i]
count[digit]--
}
// 将有序结果复制回原数组
copy(arr, output)
}
- 每一轮排序:O(n),使用计数排序对每一位进行排序。
- 总轮数:k 轮,其中 k 是最大数字的位数。
- 总时间复杂度:O(n * k)。
参考:https://www.runoob.com/w3cnote/ten-sorting-algorithm.html